Chemical equation
A chemical equation is the symbolic representation of a chemical reaction where the reactant entities are given on the left hand side and the product entities on the right hand side.[1] The coefficients next to the symbols and formulae of entities are the absolute values of the stoichiometric numbers. The first chemical equation was diagrammed by Jean Beguin in 1615.[2]
Contents |
Form
A chemical equation consists of the chemical formulas of the reactants (the starting substances) and the chemical formula of the products (substances formed in the chemical reaction). The two are separated by an arrow symbol ( , usually read as "yields") and each individual substance's chemical formula is separated from others by a plus sign.
, usually read as "yields") and each individual substance's chemical formula is separated from others by a plus sign.
As an example, the formula for the burning of methane can be denoted:
- CH4 + 2 O2
 CO2 + 2 H2O
CO2 + 2 H2O
This equation would be read as "CH four plus O two yields CO two and H two O." But for equations involving complex chemicals, rather than reading the letter and its subscript, the chemical formulas are read using IUPAC nomenclature. Using IUPAC nomenclature, this equation would be read as "methane plus oxygen yields carbon dioxide and water."
This equation indicates that oxygen and CH4 react to form H2O and CO2. It also indicates that two oxygen molecules are required for every methane molecule and the reaction will form two water molecules and one carbon dioxide molecule for every methane and two oxygen molecules that react. The stoichiometric coefficients (the numbers in front of the chemical formulas) result from the law of conservation of mass and the law of conservation of charge (see "Balancing Chemical Equation" section below for more information).
Common symbols
Symbols are used to differentiate between different types of reactions. To denote the type of reaction[1]:
- "
 " symbol is used to denote a stoichiometric relation.
" symbol is used to denote a stoichiometric relation. - "
 " symbol is used to denote a net forward reaction.
" symbol is used to denote a net forward reaction. - "
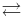 " symbol is used to denote a reaction in both directions.
" symbol is used to denote a reaction in both directions. - "
 " symbol is used to denote an equilibrium.
" symbol is used to denote an equilibrium.
Physical state of chemicals is also very commonly stated in parentheses after the chemical symbol, especially for ionic reactions. When stating physical state, (s) denotes a solid, (l) denotes a liquid, (g) denotes a gas and (aq) denotes an aqueous solution.
If the reaction requires energy, it is indicated above the arrow. A capital Greek letter delta ( ) is put on the reaction arrow to show that energy in the form of heat is added to the reaction.
) is put on the reaction arrow to show that energy in the form of heat is added to the reaction. 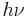 is used if the energy is added in the form of light.
is used if the energy is added in the form of light.
Balancing chemical equations
The law of conservation of mass dictates the quantity of each element does not change in a chemical reaction. Thus, each side of the chemical equation must represent the same quantity of any particular element. Similarly, the charge is conserved in a chemical reaction. Therefore, the same charge must be present on both sides of the balanced equation.
One balances a chemical equation by changing the scalar number for each chemical formula. Simple chemical equations can be balanced by inspection, that is, by trial and error. Another technique involves solving a system of linear equations.
Ordinarily, balanced equations are written with smallest whole-number coefficients. If there is no coefficient before a chemical formula, the coefficient 1 is understood.
The method of inspection can be outlined as putting a coefficient of 1 in front of the most complex chemical formula and putting the other coefficients before everything else such that both sides of the arrows have the same number of each atom. If any fractional coefficient exist, multiply every coefficient with the smallest number required to make them whole, typically the denominator of the fractional coefficient for a reaction with a single fractional coefficient.
As an example, the burning of methane would be balanced by putting a coefficient of 1 before the CH4:
- 1 CH4 + O2
 CO2 + H2O
CO2 + H2O
Since there is one carbon on each side of the arrow, the first atom (carbon) is balanced.
Looking at the next atom (hydrogen), the right hand side has two atoms, while the left hand side has four. To balance the hydrogens, 2 goes in front of the H2O, which yields:
- 1 CH4 + O2
 CO2 + 2 H2O
CO2 + 2 H2O
Inspection of the last atom to be balanced (oxygen) shows that the right hand side has four atoms, while the left hand side has two. It can be balanced by putting a 2 before O2, giving the balanced equation:
- CH4 + 2 O2
 CO2 + 2 H2O
CO2 + 2 H2O
This equation does not have any coefficients in front of CH4 and CO2, since a coefficient of 1 is dropped.
Ionic equations
An ionic equation is a chemical equation in which electrolytes are written as dissociated ions. Ionic equations are used for single and double displacement reactions that occur in aqueous solutions. For example in the following precipitation reaction:
-
- CaCl2(aq) + 2AgNO3(aq)
 Ca(NO3)2(aq) + 2AgCl(s)
Ca(NO3)2(aq) + 2AgCl(s)
- CaCl2(aq) + 2AgNO3(aq)
the full ionic equation would be:
-
- Ca2+ + 2Cl− + 2Ag+ + 2NO3−
 Ca2+ + 2NO3− + 2AgCl(s)
Ca2+ + 2NO3− + 2AgCl(s)
- Ca2+ + 2Cl− + 2Ag+ + 2NO3−
and the net ionic equation would be:
-
- 2Cl−(aq) + 2Ag+(aq)
 2AgCl(s)
2AgCl(s)
- 2Cl−(aq) + 2Ag+(aq)
or, in reduced balanced form,
-
- Ag+ + Cl−
 AgCl(s)
AgCl(s)
- Ag+ + Cl−
In this aqueous reaction the Ca2+ and the NO3− ions remain in solution and are not part of the reaction. They are termed spectator ions and do not participate directly in the reaction, as they exist with the same oxidation state on both the reactant and product side of the chemical equation. They are only needed for charge balance of the original reagents.
In a neutralization or acid/base reaction, the net ionic equation will usually be:
-
- H+ + OH−
 H2O
H2O
- H+ + OH−
There are a few acid/base reactions that produce a precipitate in addition to the water molecule shown above. An example would be the reaction of barium hydroxide with phosphoric acid because the insoluble salt barium phosphate is produced in addition to water.
Double displacement reactions that feature a carbonate reacting with an acid have the net ionic equation:
-
- 2 H+ + CO32−
 H2O + CO2
H2O + CO2
- 2 H+ + CO32−
If every ion is a "spectator ion", then there was no reaction, and the net ionic equation is null.
References
- ^ a b IUPAC. Compendium of Chemical Terminology, 2nd ed. ISBN 0-9678550-9-8.
- ^ Crosland, M.P. (1959). "The use of diagrams as chemical 'equations' in the lectures of William Cullen and Joseph Black". Annals of Science 15 (2): 75–90.
External links
- Master of Chemical Equations - Real chemical equation balancer.
- Chemical Equation Balancer - An open source chemical equation balancer.
- Classic Chembalancer - Play Chembalancer, a free online game at FunBasedLearning.com, to learn how to balance equations by inspection
- Online calculator, determines of the coefficients of a chemical equation
- Online Chemical Equation Balancer Balances equation of any chemical reaction (full or half-cell) in one click.
- Balance chemical equations Teaches how to balance chemical equations
- Stoichiometry Add-In for Microsoft Excel for calculation of molecular weights, reaction coëfficients and stoichiometry.